October 30, 2020 [product]

「白銀箸」　点対称の柱体で造形された箸。
簡素な構造で、どの面で持っても掴みやすく、
直径の太い部分を支点にする事で、しっかり掴めます。

　柱体の重心を箸の頭部分に置き、傾斜を利用して倒すことで、箸先を浮いた状態にしています。 　箸先を浮かす形は幾つかありますが、４面のどの面で置いても同じ効果が得られる点で、目的は同じであっても、原理が異なっています。

　持ち代は、４回転対称の柱体で、転がりにくく安定します。 　支点部分は八角形で、角の引っ掛かりを軽減します。 　箸先は四角形で、面と角で滑りにくく、小さな物も掴めます。 　使い代は、箸先まで直線で削られており、均等にしっかり掴めます。
　支点の位置、指の位置を変えることで、自分に合った角度で箸を持てます。 　八角形の部分を中心に短め、普通、長め、の３種類の持ち方が出来ます。

haku001

download

haku001.pdf

・白銀箸（はくぎんばし）

・持ち手の位置を変えることで、自分に合った角度で箸を持てます。
　支点を中心に短め、普通、長め、の３種類の持ち方が出来ます。

・回転対称の柱体で造形された箸。簡素な構造で、
　どの面で持っても掴みやすく、
　直径の太い部分を支点にする事で、しっかり掴めます。

・箸の重心を持ち代に置き、傾斜を利用して傾けることで、
　箸先を浮いた状態にしています。
　箸先を汚さずに置くことができます。
　柱体のどの面で置いても同じ効果が得られます。

・箸先を浮かす方法は幾つかありますが、
　支点からの傾斜を利用した方法は独自性があり、
　目的は同じであっても、原理が異なっています。

・持ち代は、４回転対称の柱体で、転がりにくく安定します。
　支点部分は八角形で、箸同士の角の引っかかりを軽減します。

・持ち代の支点までの傾斜が、指の滑りを軽減します。

・箸先は四角形で、面と角で滑りにくく、小さな物も掴めます。
　使い代は、箸先まで直線で削られており、均等にしっかり掴めます。

・ペンで文字を書く時もそうですが、箸も回転させながら持ち直して
　います。回転対象の柱体は持ち直しが容易です。

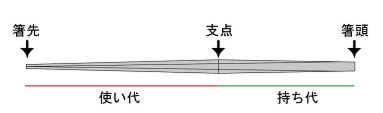
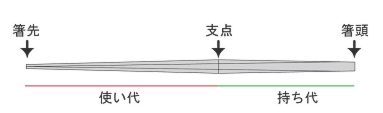
　箸の頭部分が細くなる様に傾斜がかかっている為、
箸を広げても、頭部分が接触しません。

・支点と箸先の直径、持ち代の長さの３点を決めると全体の設計が出来ます。
・√2（白銀比）を使った計算式のみで構成されています。
・使い代と持ち代の比重は、約　1：1.31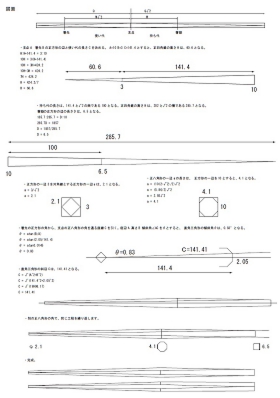

download

haku017.pdf

　持ち代が細い場合、面取り無しの四角形の選択も有り。
その場合は、使い代　部分と　持ち代　部分の重量差が微量になる。
　安定させる為には、箸先から支点の持ち代までを軽量化（削り）
する必要がある。

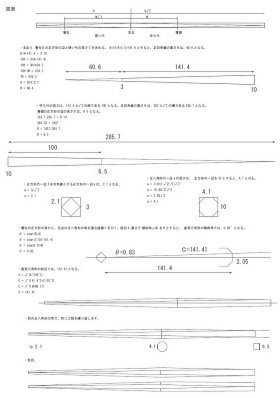
備考

正八角形の面積　正八角形の一辺 a　正方形の一辺の半分 b
S=(a8)b/2
正四角錐台の体積　底辺の長さ a　上辺の長さ b　高さ h
V=1/3 (a^2 +ab+b^2 )h
四角錐台の体積　底辺の長さ AとB 上辺の長さ aとb　高さ h
V=h/6(Ab+Ba+2(AB+ab))
角錐台の体積　上面積 S1　底面積 S2　高さ h
V=h/3 (S1 +S2+√(S1S2))

白銀比　1：√2　
正八角形の一辺a　　正方形の一辺 A
a=(A(2-√2)/2)√2
直角三角形の斜辺　底辺 a　高さ b　斜辺 c
c=√(a^2+b^2)
直角三角形の底辺Aと高さBから傾斜角θ(∠AC)
θ=atan(B/A)

haku014

download

haku014.pdf

top